Before we begin with the mathematics we should start first by defining the problem and the terms associated with it. Image inpainting is the reconstruction of a corrupted or damaged image through some means. In this post I will be discussing an interesting method that can be used to reconstruct an image based on a signal processing technique known as compressed sensing which can yield decent results.

Low-rank Matrix Completion

Before we can reconstruct the damaged image we start by considering the image in a simpler form: as a matrix of pixel values. From this we see that reconstructing an image can be viewed as the reconstruction of a generic matrix. Unfortunately, as you may have guessed it is generally impossible to reconstruct a generic matrix given nothing except that it has been corrupted in several places. However, we can still reconstruct some matrices given certain assumptions about the matrices.

The particular assumption we consider is that of low-rank. This actually is a pretty decent assumption to make in a lot of modern settings. For example, many social networks can be represented by sparse low-rank matrices. In addition, the famous Netflix Problem involves a matrix of Netflix users against their movie ratings which forms an inherently sparse low-rank matrix (most people have not watched and rated every show on Netflix). This new problem we have formed can be written more formally as:

$\underset{X}{\min} \text{ } rank(X) \text{ , s.t. } X_{ij} = M_{ij} \text{, } \forall (i,j) \in \Omega$

Where $X$ is the matrix that we are trying to reconstruct, $M$ is target Matrix we are trying to reconstruct to, and $\Omega$ is the set of indices in the given $X$ matrix that we known are uncontaminated/undamaged.

Reconstructing a matrix under this assumption that the matrix is of low-rank is actually possible; however, it is computationally intractable and thus isn’t particularly useful in most settings that we would like to use it for. If you want to fix your image you don’t want to wait 5 hours for it to reconstruct, you want it fixed quickly. To solve this issue we can slightly modify our equation to instead minimize the nuclear norm of the matrix.

The Nuclear Norm of a matrix is the sum of the absolute values of its singular values and is represented by $||\cdot||_*$. You can also think of this as applying the $\ell_1$ norm to the singular values of $X$. Through a series of mathematical arguments it has been shown that this nuclear norm is a good approximation for the rank of a matrix. This is fortunate because there do exist computationally tractable methods for solving this new problem which we formally define as follows.

$\underset{X}{\min} \text{ } ||X||_* \text{ , s.t. } X_{ij} = M_{ij} \text{, } \forall (i,j) \in \Omega$

At this point we have finally arrived at the problem of tractable low-rank matrix completion. This particular problem can now be solved using a couple of different efficient optimization methods including the ADMM method which is a subset of the Augmented Lagrangian Methods.

Image Inpainting

So we starting discussing an image and ending up discussing low-rank matrices but how exactly does this information help us? As you may have thought, images are inherently neither sparse nor low-rank; however, we can apply a signal transform to make a given image sparse.

An example transformation we may apply to the image is the fourier transform (or in our case discrete fourier transform) which decomposes a given function (the image in our case) into its constituent frequencies (sines and cosines) that make it up. If you’re having difficulty visualizing how an image can be a function that can be broken up into different frequencies first consider a grayscale image and then think of it as a surface embedded in $\mathbb{R^3}$. Image it with its x,y values being the x,y pixel coordinates in the image and the z value being the numerical brightness value associated with that pixel (similar to a heatmap). We can take the following image as an example:

which when plotted as a surface embedded in $\mathbb{R^3}$ looks like a sine wave as seen below:
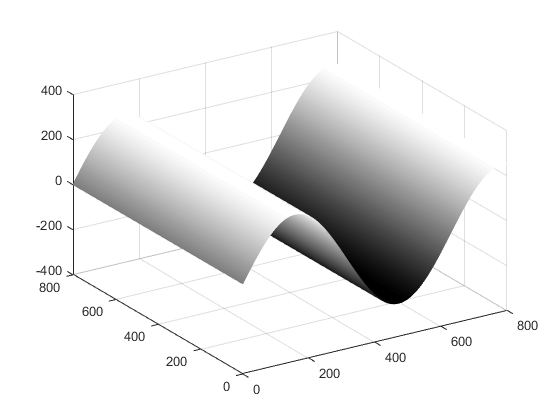
So once we visualize the image as a function we can apply a signal transform to function. For reconstructing images we will actually apply a lesser known transform known as the wavelet transform because it tends to create sparser representations of images. After applying the wavelet transform we can then take the transformed image (which will be sparse) and utilize our tools from low-rank matrix reconstruction to reconstruct it. So we now have a reconstructed “wavelet” image which can be converted back to look like an image we want by simply applying an inverse wavelet transform.

Results

Using this technique we can actually obtain some surprisingly good results. I wrote a program that uses the techniques discussed above to reconstruct a couple of images that have had text placed over them (effectively obscuring a large portion of the images). Specifically, I considered the reconstruction of the classic Barbara image:

I also additionally reconstructed an image of cameraman as you can see below:

As you can see this method provides a decent way to reconstruct images that are largely obscured. Both of these reconstructions were done by setting up the optimization problem as discussed and iteratively solving it using the ADMM optimization method. If you want to know more details regarding how exactly this is done you can download the following paper I wrote describing it in more detail.